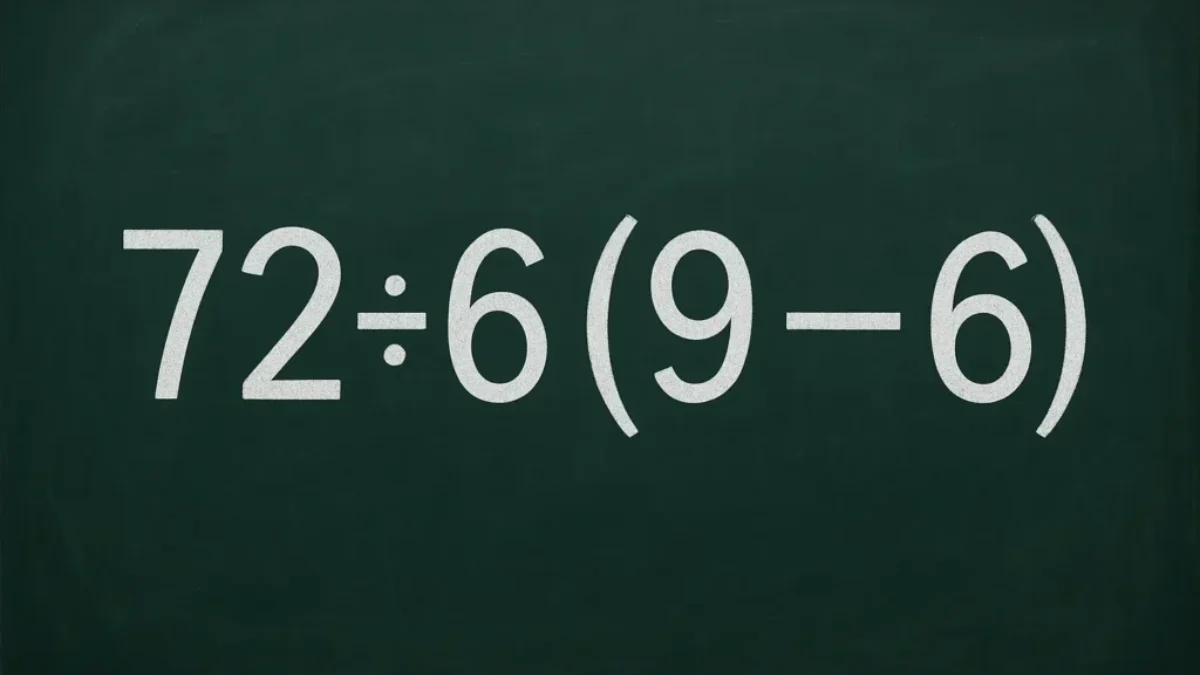Tento příklad přivádí uživatele internetu k šílenství. Kolik je 72 : 6 (9 − 6) zmátlo i ty nejbystřejší

Toto je typ zdánlivě jednoduchého matematického příkladu, který poslední dobou koluje internetem a vzbuzuje vášnivé debaty i rozpory. Proč tomu tak je? Důvodem je nejednoznačnost v interpretaci zápisu, která vyvolává zmatky ve správném pořadí provádění matematických operací v něm. Jde hlavně o dělení a násobení, které jsou zapsány bez jasných závorek. Tak co s tím?

Pokud si nepamatujete ze školy, jaké operace mají v příkladu přednost, narazíte. Ale nebojte, nejste v tom sami. Problém s pořadím jednotlivých operací má většina těch, co jsou už nějaký ten pátek ze školy. My vám ale prozradíme, jak správně příklad 72 : 6 (9 − 6) vyřešit.

Příklad, který má na internetu mnoho interpretací

Náš konkrétní příklad je na internetu často uváděn k vyřešení – a pod příspěvkem se v komentářích objevují různé tipy na výsledek. Svým nejednoznačným zápisem zapříčinil vzplanutí emocí na mnoha sociálních sítích a kanálech. Jde hlavně o to, že takto zapsaný příklad lidi mate a ti ho řeší různými způsoby. Zápis v matematice znamená vše. Někdo čte příklad jako [72 : 6] × (9 − 6), někdo zase 72 : [6 × (9 − 6)]. A to, jak příklad čtete, má vliv na výsledek, ke kterému dojdete.

„Nikdo nikdy v matematice, která je aspoň trochu na úrovni, nepoužívá děleno. Od toho jsou zlomky, “ objevuje se v diskuzích.

Stejně tak:

„Můj bývalý matikář by mi to prostě omlátil o hlavu jako nejasně zadaný příklad a řekl, ať přidám závorky nebo to hodím do zlomku, tedy aby zadání opravdu nebylo nejednoznačné.“

Nejeden člen podobných diskuzí vyjadřuje svou frustraci z nepřesného zápisu. A pak není jasné, co přesně po nás zadání chce. To vede k vícero možným výsledkům a k bohatým debatám ohledně matematických pravidel.

Internetem kolují dva možné výsledky: 36 a 4

Nejběžnější výsledky internetových přispěvovatelů pro příklad 72 : 6 (9 − 6) jsou 36 a 4 a kolikrát se objevují i docela jiné hodnoty. Rozpor, který vzniká, má jasnou příčinu – interpretaci.

Číslo 36 dostanete, když se řídíte zaběhlými pravidly pořadí operací, ve kterém má dělení a násobení stejnou prioritu a vypočítává se zleva doprava: 72 : 6 = 12, pak 12 × 3 = 36.

K hodnotě 4 se dostanete, když upřednostníte zápis 72 : [6 × (9 − 6)], tedy pokud dělíte 72 celým číslem, které je produktem zápisu 6 × (9 − 6). Takže 72 : (6 × 3) = 72 : 18 = 4.

Jak je to správně?

Nejdřív vysvětlení pravidel

Matematika má svá jasná pravidla, a ta je potřeba dodržovat, abychom dosáhli správných a také jednoznačných výsledků. Díky nim přesně víme, v jakém pořadí se řeší závorky, mocniny, dělení, násobení, sčítání a odčítání.

Při výpočtu mají nejvyšší prioritu závorky, takže se nejdříve vypočítávají výrazy uvnitř nich. Poté následuje dělení a násobení, které jsou na stejné úrovni. Nesprávné pochopení tohoto pravidla, například pokud předpokládáte, že násobení vedle závorky je v našem příkladu prioritou před dělením, vede k nesprávným výsledkům. A my vám teď konečně vysvětlíme, kdo se v internetových diskuzích trefil do správného výsledku a kdo ostrouhal.

Správné řešení příkladu 72 : 6 (9 − 6)

Držte si klobouky, odhalíme správné řešení příkladu 72 : 6 (9 − 6), a to krok za krokem.

Nejdříve je potřeba vyřešit závorku: 9 − 6 = 3

Příklad se tak změní na: 72 : 6 × 3

Dělení a násobení mají ve standardních pravidlech stejnou prioritu, jinak se provádějí zleva doprava. Nejprve tedy provedeme dělení: 72 : 6 = 12

Pak vynásobíme výsledkem z kroku 3, tedy 12 × 3 = 36

Správný výsledek příkladu 72 : 6 (9 − 6) je tedy 36. Tento příklad ukazuje, jak je důležité dobře rozumět pravidlům priorit operací zápisu. Postup výše si zapamatujte, a příště, až se na internetu objeví další diskuze o podobném příkladu, už budete vědět, jak ho správně vyřešit.