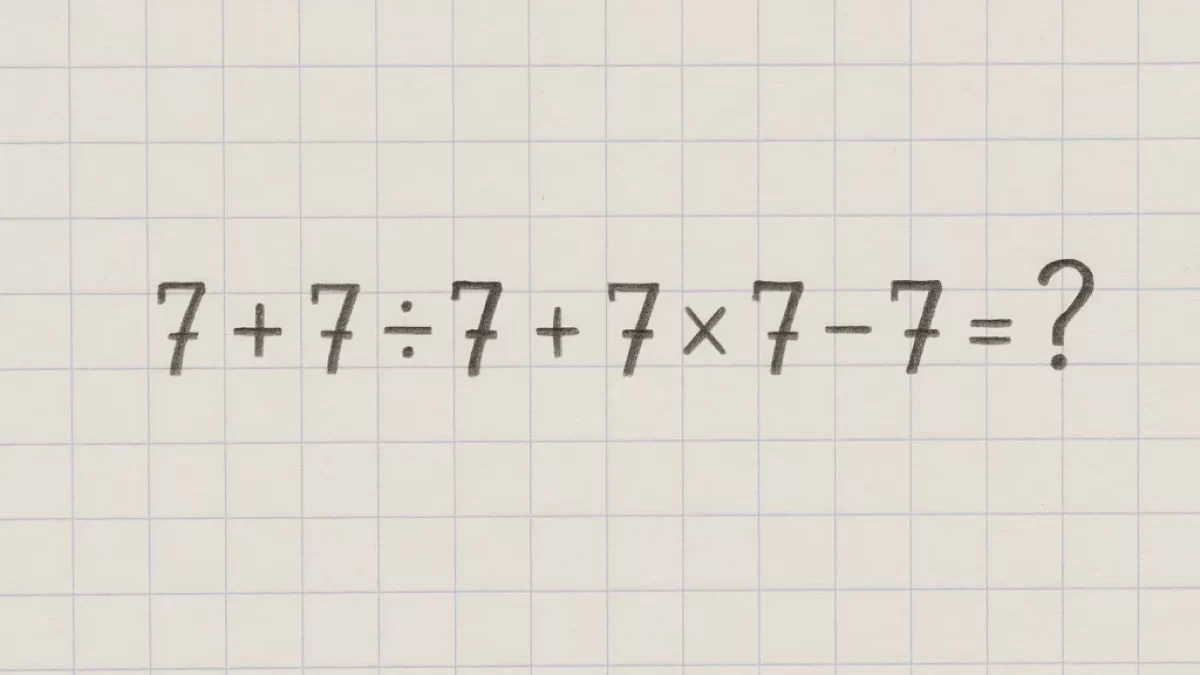Spočítat 7 + 7 ÷ 7 + 7 × 7 – 7 zvládne i malé dítě. Dospělí přepisují výsledek 3× a pořád špatně. Dáte to?

Matematika nás doprovází dennodenně, i když si to možná ani neuvědomujeme. Někdy nás ale může i zdánlivě jednoduchý výpočet pořádně vykolejit. Je příklad 7 + 7 ÷ 7 + 7 × 7 – 7 taková brnkačka, nebo se necháte nachytat?

Matematika nemusí být nuda, byť některé její části skutečně nejsou úplně nejzajímavější. Příklad 7 + 7 ÷ 7 + 7 × 7 – 7 by měl každopádně zvládnout spočítat každý. Jenže to nemusí být zase taková brnkačka, jak by se mohlo na první pohled zdát. Než se však pustíme do jeho výpočtu, zaměříme se na některá zajímavá fakta, která se týkají právě počítání. Půjde vám z nich hlava kolem!

Proč je číslo 10 výjimečné?

Myslíte si, že čísla jako 10, 20, 30 atd. jsou nějak výjimečná přirozeně? Vlastně nejsou. Výjimečná jsou jen proto, že teď a tady používáme desítkovou soustavu. Proč právě desítkovou? To se neví. Pravděpodobně však hrál zásadní roli počet lidských prstů. Z toho ovšem vyplývá, že pokud by měl člověk čtyři prsty na každé ruce, považovali bychom za výjimečná čísla 8, 16, 24 atd. Ostatně desítková soustava je i podle některých matematiků poněkud nepraktická a pro počítání by byla lepší třeba soustava dvanáctková.

Počítače používají dvojkovou soustavu neboli soustavu binární, kde nacházejí uplatnění jen jedničky a nuly. Ve starověké Mezopotámii, jedné z hlavních kolébek matematiky jako takové, zase používali, kdo ví proč, šedesátkovou soustavu. Že už nám aktuálně matematika dávno mrtvého světa nemá co dát? Chyba lávky! Dodnes totiž její reprezentaci čísel stále používáme. Proč si myslíte, že má hodina 60 minut nebo plný úhel 360°? Opět nejde o nic přirozeně daného, ale jen o praktický pozůstatek starověké matematiky.

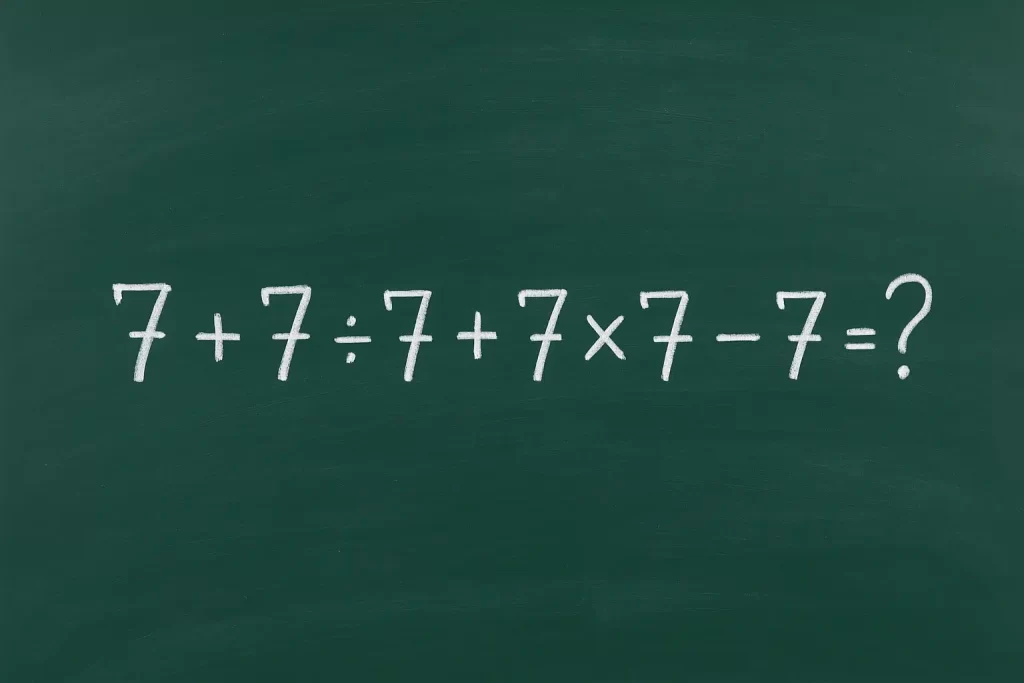
Jaké je nejvyšší číslo na světě?

Pochopitelně žádné. Pokud byste si teoreticky představili nejvyšší číslo, vždy lze myslet nejvyšší číslo plus jedna atd. Dnes mnoho lidí používá vyhledávač Google, víte ale, co je googol? Tento pojem vymyslel v roce 1938 devítiletý synovec amerického matematika Edwarda Kasnera jako označení pro hodně vysoké číslo. O jaké číslo jde konkrétně? O 10¹⁰⁰. To je jednička a sto nul. Jde o vyšší číslo, než je odhadovaný počet atomů ve viditelném vesmíru. Pojďme ovšem ještě dál.

Je-li googol velkým číslem, jak velkým číslem je googol na googol, tedy 10¹⁰⁰ na 10¹⁰⁰? Takové číslo je naprosto nepředstavitelné. Ale přece jen to zkusme. Pokud byste začali společně s Velkým třeskem, který nastal zhruba před 13,8 miliardami let, psát nuly rychlostí dvě za sekundu, dodnes byste ono číslo neměli napsané! Zní to možná šíleně, ale je to tak. Na některá matematická fakta se zkrátka a dobře perfektně hodí anglický termín „mind-blowing“, protože mohou být až nepochopitelně vzrušující.

Pro zajímavost: Zakladatelé Googlu, tedy Larry Page a Sergey Brin, skutečně použili pro název svého vyhledávače zkomoleninu termínu googol, takže podobnost obou slov není náhodná.

Kolik je 7 + 7 ÷ 7 + 7 × 7 – 7?

Po troše té matematické teorie se konečně vrhněme na náš příklad. Jeho vyřešení nemusí být zase tak složité, ale nejprve si musíme zopakovat pravidla pro prioritu matematických operací.

• Z – první počítáme závorky
• U – následně se vrhneme na umocňování a odmocňování
• NADE – pak násobíme a dělíme
• SO – na závěr sčítáme a odčítáme

Nyní se již tedy můžeme pustit do samotného výpočtu. Postupujme podle návodu výše. Nejprve vyřešíme násobení a dělení, tedy početní úkony, které mají přednost před sčítáním a odčítáním. Pak zůstává příklad v podobě 7 + 1 + 49 – 7. Následně už je vše naprosto jednoduché. Úplně elementárním výpočtem dojdeme k výsledku 50. Předpokládáme, že i přes chvilkové zaváhání došla ke stejnému číslu většina čtenářů.