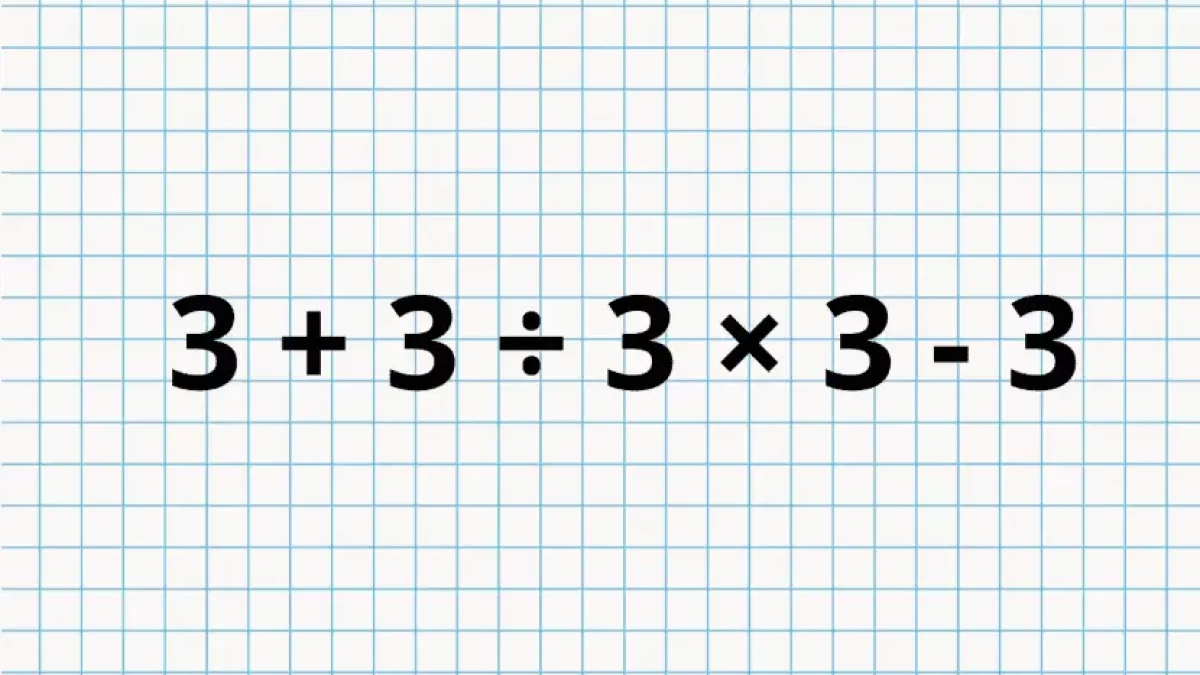Kolik je 3 + 3 ÷ 3 × 3 – 3? Tato matematická úloha potrápí i ty nejchytřejší. Zkuste ji vyřešit

Matematické úlohy jsou skvělým způsobem, jak si procvičit logické myšlení a soustředění. Často se stává, že i zdánlivě jednoduché příklady mohou být nakonec záludné, a dopídit se k výsledku není tak jednoduché, jak se na první pohled zdá.

Podobné výpočty se objevují nejen v testech inteligence, ale i v běžném životě. Je tedy dobré umět s čísly pracovat a osvojit si alespoň nutné základy pro spolehlivý výsledek i bez kalkulačky. Mnoho lidí však u příkladů, ve kterých se kombinuje hned několik operací, snadno chybuje. Přehlédnou správné pořadí nebo dají přednost intuitivnímu způsobu počítání namísto přesného postupu podle pravidel matematiky.

Příkladem takového chytáku je výraz 3 + 3 ÷ 3 × 3 – 3 → ten vypadá jednoduše, ale jeho správné řešení vyžaduje znalost základních principů výpočtů. Matematika je totiž věda založená na dodržování přesných postupů, jedině ty nás totiž dovedou až ke správnému výsledku. Dokážete bezchybně tento příklad vypočítat?

Pořadí operací v matematice – proč je tak důležité?

Dodržení správného pořadí jednotlivých operací je při řešení matematických úloh klíčové. V opačném případě totiž dojdeme ke zcela jinému, a tedy i nesprávnému výsledku. Matematika je ale exaktní věda, ve které je správná odpověď pouze jedna.

Správné pořadí výpočtů určuje několik pravidel, které se běžně učíme již na prvním stupni základní školy. Prvním krokem u podobných příkladů je vždy vypočítat závorky, jsou-li přítomny. Následuje umocňování a odmocňování, poté se přechází k násobení a dělení.

Teprve až nakonec se všechna čísla a výsledky předchozích operací sčítají a odčítají. Pokud je sčítání a odčítání v příkladu více, postupuje se již podle pořadí zleva doprava.

Jak si podobné příklady rychle vypočítat z hlavy?

Ačkoliv se může zdát, že příklad o několika úrovních výpočtů nelze spočítat z hlavy, jde o poměrně jednoduchou záležitost. Pokud dobře známe správný postup a máme trochu cviku, není problém si i bez papíru identifikovat operace s vyšší prioritou a vyřešit je jako první.

Máme-li hotové dělení a násobení, sčítání a odčítání je už hračka. Pokud si nejste jistí nebo potřebujete grafické znázornění, zkuste si příklad představit se závorkami a postupovat podle nich. Dobrá strategie je také trénovat si podobné příklady pravidelně – díky tomu si správný postup zautomatizujeme, neděláme chyby a navíc si pravidelně procvičujeme logické myšlení a bystrost.

Řešení výrazu

Nyní se podíváme na konkrétní rozbor našeho matematického výrazu 3 + 3 ÷ 3 × 3 – 3 a ukážeme si, jak správně postupovat.

Nejprve provedeme dělení: 3 ÷ 3 = 1.

Poté vynásobíme výsledek dělení číslem 3: 1 × 3 = 3.

Nyní zbývá pouze sčítání a odčítání.

Sečteme první číslo ve výrazu se získaným výsledkem: 3 + 3 = 6.

Nakonec odečteme poslední trojku: 6 – 3 = 3.

Správný výsledek tohoto výrazu je tedy 3.

Tento příklad nám krásně ukáže, jak snadné je udělat chybu. Zejména pokud si nedáme dobrý pozor na to, které výpočty mají přednost a nepostupujeme podle základních matematických pravidel.

Jak se zlepšit v matematice?

Pravidelný trénink je klíčem k úspěchu. I když už nepatříte mezi žáky školou povinné, procvičování matematiky a zlepšení svých schopností bychom se měli věnovat i po zbytek života. Díky tomu nezapomeneme na výše zmíněná základní pravidla a procvičíme i svou mysl.

Pokud vám matematika nikdy nešla, nezoufejte, naučit se ji totiž může každý. Jediný rozdíl je v tom, že některým stačí procvičovat občas, a jiní naopak potřebují pravidelnost a neustálé opakování, aby si postupy osvojili a zapamatovali.

Procvičování matematických příkladů ale není jen o počtech, které zrovna nevyužijete. Díky tomuto „cvičení mozku” se zlepšíte v řešení složitějších problémů, budete mít rychlejší odhad například při nákupech, zlepšíte svou schopnost věci správně analyzovat a vyhodnotit. Mentální trénink je totiž podobně důležitý jako ten fyzický.