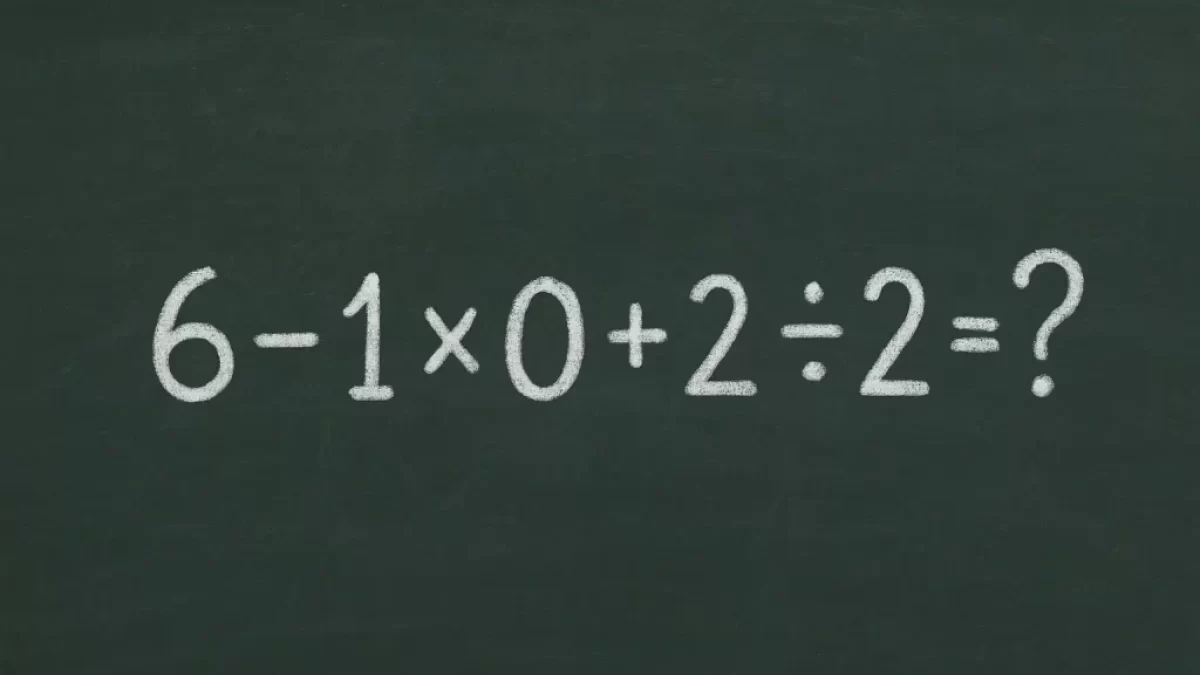Tento jednoduchý příklad dnes zmate i vysokoškoláka: 6 – 1 × 0 + 2 ÷ 2 = ? Schválně, dáte to správně?
Mohlo by se zdát, že některé matematické příklady musí správně spočítat snad každý. Jenže ve skutečnosti to tak jednoznačné není. Spousta lidí dnes selhává i při poměrně banálních výpočtech. Není tedy divu, že si matematici rvou vlasy.
Říkáte si, že příklad 6 – 1 × 0 + 2 ÷ 2 spočítáte levou zadní? Někteří lidé se při tomto zadání škrábou na hlavě a za výsledek by od učitele dostali čistou pětku. Každému počtáři na internetu totiž vychází jiné číslo. Někdo tvrdí, že je to pět, další sedm a další jedna. Příklad se tak stal na internetu virálním. Jasně totiž ukazuje, že se bez elementárních znalostí matematiky základní školy neobejdeme. Respektive asi obejdeme, ale tyto vědomosti nám mohou dost usnadnit spoustu každodenních aktivit.
25 + 18 na kalkulačce?
Počítání je jedna ze základních věcí, kterou se děti učí na základních školách. Zvládnout elementární početní úkony by tedy měl v podstatě každý, kdo dokončil povinnou školní docházku. Mnozí lidé však i nejjednodušší příklady počítají na kalkulačce. Tu dnes má ostatně každý při ruce na mobilu. Tak proč se trápit? I při počítání na tomto zařízení je ovšem nutné znát některá základní matematická pravidla. V našem příkladu například správné pořadí početních operací. Budete-li totiž postupovat jednoduše zleva doprava, rozhodně vám nevyjde správný výsledek.

Zvládli byste ještě trojčlenku?
Podle odborníků je základem všeho trojčlenka. Pokud se někoho zeptáte, co si pamatuje z matematiky základní školy, trojčlenka bude pravděpodobně velice častou odpovědí. Využít ji totiž můžeme i v běžném životě, a to třeba při nakupování. Pokud například 5 kg jablek stojí 150 korun, kolik bude stát 7 kg tohoto ovoce? Jednoduše trojčlenkou dojdeme k tomu, že 1 kg jablek stojí 30 korun, takže 7 kg musí nutně stát 210 korun. Není to tedy vůbec nic složitého a může nám to velmi pomoci při návštěvě večerky na rohu či supermarketu.
Malujeme s matematikou
Matematika se nám hodí i jinde. Máme-li třeba místnost bez oken se stěnami o délce 5 a 7 metrů a o výšce 2,5 metru, kolik budeme potřebovat barvy na její vymalování? Povrch kvádru jednoduše spočítáme tak, že sečteme obsahy všech obdélníků, které ho tvoří. Vzorec? S = 2 (ab + ac + bc). Ovšem pozor! V případě malování jde o jistý chyták. Skutečně totiž potřebujeme vymalovat všechny stěny? Stěny (a strop) ano, ale podlahu asi malovat nebudeme. V naší situaci tedy bude vzorec S = ab + 2ac + 2bc. Po dosazení spočítáme, že budeme potřebovat barvu na 95 metrů čtverečních.

Kolik je 6 – 1 × 0 + 2 ÷ 2?
Pro výpočet našeho příkladu je nutné znát především jedno pravidlo, a to pro prioritu početních operací. Jednoduše zleva doprava totiž postupovat nelze. Toto pravidlo se přitom nazývá ZUNADESO. Co že je to za podivný název? Jde o zkratku jednotlivých početních úkonů. Nejprve tedy spočítáme Závorky a uděláme Umocňování, což ale pro náš příklad není důležité. Pak se musíme vrhnout na NÁsobení a DĚlení a až na úplném konci na Sčítání a Odčítání. Jak tedy budeme postupovat?
- Nejprve vynásobíme jedničku a nulu a vydělíme dvě dvojky na konci.
- Nyní máme příklad 6 – 0 + 1, což už jednoduše spočítáme a vyjde nám samozřejmě 7.
Jiná správná odpověď opravdu neexistuje, a pokud se domníváte, že v takovémto příkladě nemohl nikdo chybovat, jste na omylu. Budeme-li například postupovat zleva doprava, vyjde nám jedna. Dalším lidem vychází pět. Pokud si každopádně myslíte, že matematika je vašim dětem k ničemu, protože ani vy sami ji ve svém životě nijak nevyužíváte, možná není od věci tento názor změnit. Jak jsme si koneckonců ukázali, znalost základů matematiky nám skutečně může usnadnit spoustu každodenních situací.