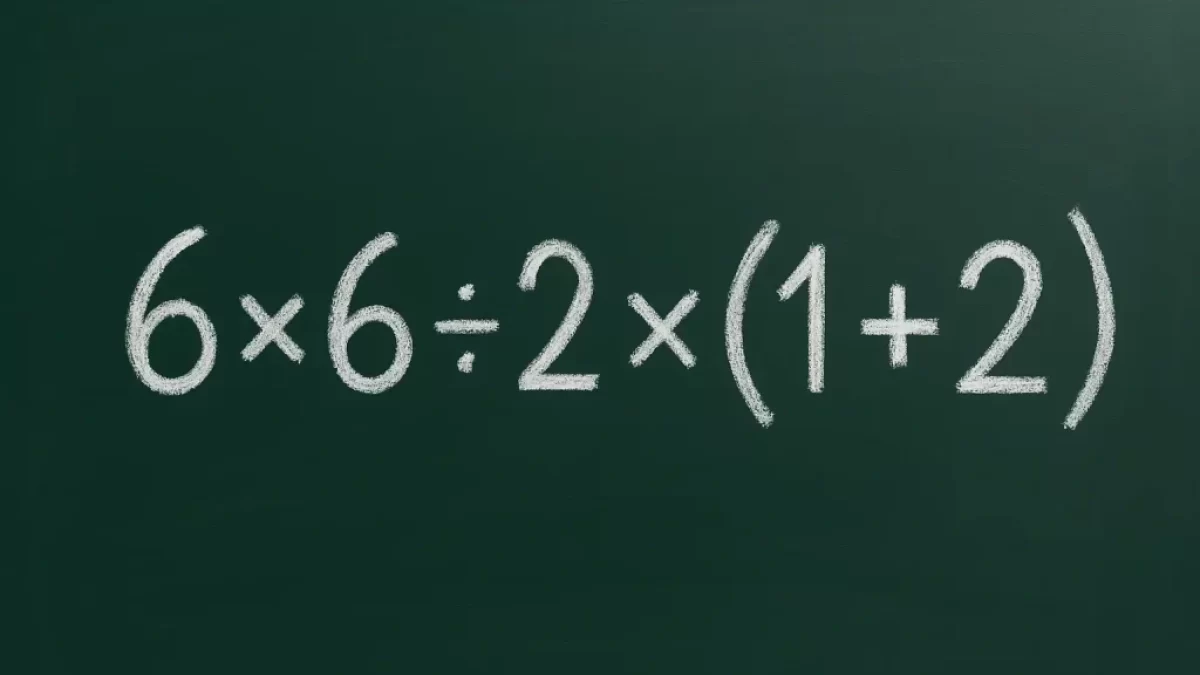Nejspornější příklad internetu: 6 × 6 ÷ 2× (1 + 2). Vypadá snadně, ale milionům lidí zavaří mozek

Kolik je 1 + 1, ví asi každý. Jenže existují matematické příklady, které vypadají zdánlivě snadně, ale pokud se do nich pustíte, můžete si na nich poměrně jednoduše „vylámat zuby“. Dokážete spočítat, kolik je 6×6 ÷ 2× (1+2)?

Matematika pro většinu z nás skončila s posledním zazvoněním ve škole. Přesto bychom jisté základy počítání měli zvládat i dávno poté, co jsme opustili školní škamny. Jednoduché aritmetické úlohy dokáže vyřešit i v pokročilejším věku asi každý, jenže problém může nastat u počtů, při kterých jsou ve hře závorky a větší množství znamének. Náš příklad 6 × 6 ÷ 2× (1 + 2) tedy může zmást i chytráky. Ti méně bystří pak udělají chybu, která je zavede k naprosto špatnému výsledku.

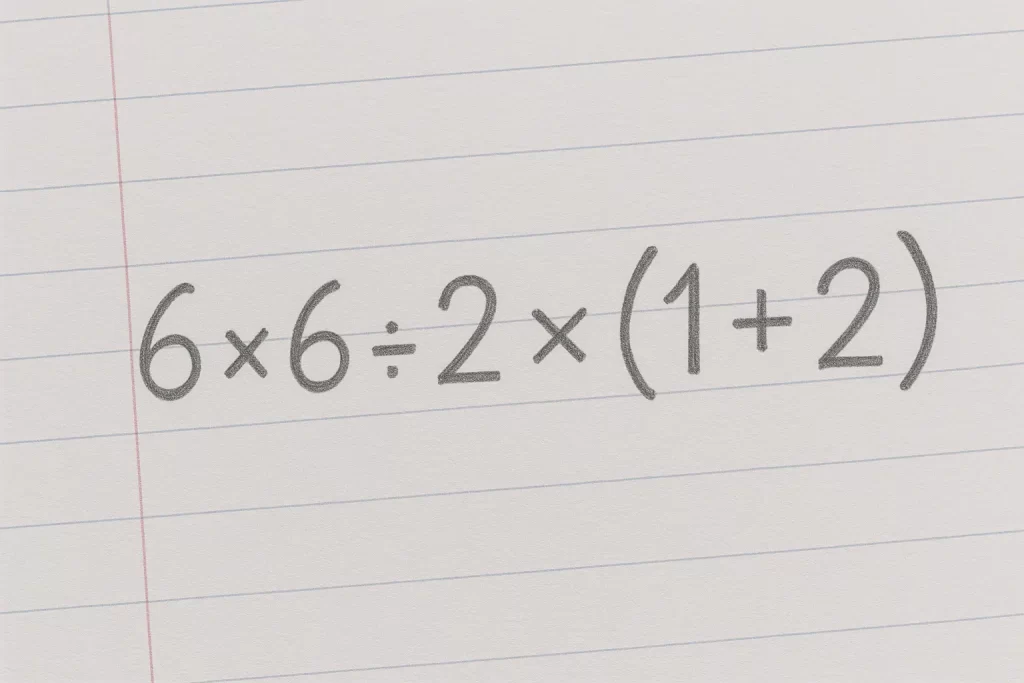
Jaká jsou pravidla pro správné počítání?

Předně si je nutné uvědomit, jaké je správné pořadí početních operací. Každý si asi ještě ze školy pamatuje, že násobení má přednost před sčítáním. Náš příklad je ale přeci jen zapeklitější. Můžeme tak skutečně dojít ke zcela rozdílným výsledkům. Stačí ovšem, když si i do budoucna zapamatujete spojení ZUNADESO. Ne, není to nesmysl. Naopak se jedná o užitečný akronym, který pomáhá zapamatovat si přesné pořadí matematických operací. Jak konkrétně?

• Z – první počítáme závorky
• U – následně je na řadě umocňování a odmocňování (tato informace je pro náš příklad jako jediná zbytečná)
• NADE – poté násobíme a dělíme (žádná z těchto početních operací nemá přednost před druhou)
• SO – nakonec sčítáme a odčítáme (ani v tomto případě není určena žádná přednost)

Vrhněme se konečně na náš příklad

Známe-li tedy pravidla, můžeme jednoduše vypočítat zadaný příklad. Pracujme postupně. Musíme ovšem ještě zdůraznit, že při základních aritmetických výpočtech se postupuje zleva doprava.

• 6 × 6 ÷ 2 × 3 – pokud není za číslem před závorkou znaménko, bere se to jako krát
• 36 ÷ 2 × 3 – postupujeme zleva doprava!
• 18 × 3 – tohle už zvládne spočítat každý

Nyní je již zjevné, že správným výsledkem je číslo 54. Pokud vám tedy vyšlo něco jiného, měli byste si možná zopakovat své matematické znalosti. V našem příkladu lze ovšem učinit v podstatě jen jednu jedinou chybu. Někteří počtáři totiž v jednotlivých krocích nepostupují zleva doprava, takže jim v posledním kroku vyjde 36 ÷ 6 a výsledek 6. Jde tedy o zcela jiné číslo.

Vše si správně spočítat může být zásadní

Je to tak. Může nás o tom koneckonců přesvědčit starý příběh. Jeden indický král se rozhodl jistého učence odměnit za to, že vymyslel jeho oblíbenou hru, totiž šach. Ten ovšem k překvapení panovníka nechtěl peníze, ale rýži či pšenici (v tom se příběhy liší). Učenci stačilo, když se na první pole šachovnice umístí jedno zrnko, na druhé dvě, na třetí čtyři, na čtvrté osm atd. Král s tím souhlasil a myslel si, jak učenec prohloupil. Ovšem jen do té doby, než mu údajný vynálezce šachu kompletně vyprázdnil sýpky v zemi a vzkázal mu, že si pro zbytek své odměny pošle později.

Matematicky lze učencův požadavek vyjádřit takto: 2⁰ + 2¹ + 2² + 2³ atd., a to až po 2⁶³ (šachovnice má sice 64 políček, ale začínáme jedním zrníčkem, což je skutečně 2⁰). Výpočtem nám následně vyjde, že pouze samotné 2⁶³ představuje zhruba 18 trilionů zrnek! Ani 2⁶² či 2⁶¹ přitom nejsou právě nejmenším množstvím. Učenec tedy vyzrál na krále, a ne naopak. Jak si tak obrovské množství představit? Pokud bychom chtěli výsledný objem rýže či pšenice odvézt vlakem, tak by musel mít čtyři miliardy vagónů!  Inu, správné a přesné počítání může být někdy opravdu podstatné.